RANDOM PAGE
SITE SEARCH
LOG
IN
SIGN UP
HELP

Truth Tables

This is the AQA version closing after June 2019. Visit the the version for Eduqas instead .

To gain access to revision questions, please sign up and log in.

Everyone

Learn This

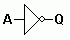
Logic Gates Summary :: Learn all the details in the table below including ...

The Gate Symbols.
The Boolean Notation.
The Plain English Rules. - Especially learn the yellow highlights.
The Truth Tables (Two Styles) - Especially learn the yellow highlights.

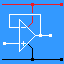
AND

NAND

NOR

XOR

NOT

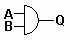
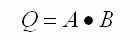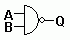
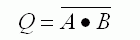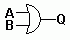
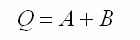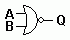
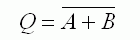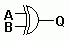
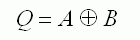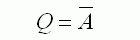Two ones give a one.
Anything else gives 0.

Two ones give a 0.
Anything else gives 1.

Two zeros give a 0.
Anything else gives 1.

Two zeros give a 1.
Anything else gives 0.

Equal inputs give a 0.

Input is inverted.

A  Q
0  1
1  0

_B\^A	0	1
0	0	0
1	0	1

_B\^A	0	1
0	1	1
1	1	0

_B\^A	0	1
0	0	1
1	1	1

_B\^A	0	1
0	1	0
1	0	0

_B\^A	0	1
0	0	1
1	1	0

A	0	1
Q	1	0

Logic Levels

	CMOS 4000 Series Chips	TTL 7400 Series Chips	Commonly Used Terms
Technology	Complementary Metal Oxide Semiconductor	Transistor Transistor Logic
LOW	A voltage less than 0.5 of the power supply	0 to 0.8 V	0, Zero, Off, Clear, False
HIGH	A voltage greater than 0.5 of the power supply	2.2 to 5 V	1, One, On, Set, True
Power	Extremely low power consumption	High power use compared with CMOS
Speed	Slower	Faster

Logic Goats

Logic Goats :: Logic Gates Exercise

Falstad Circuit Simulations

These simulations are excellent for building logic and other circuits. This simulator can be used on-line or downloaded. Either way you will need to install the Java Run-Time Environment if it is not already on your computer.

For the Falstad Circuit Simulation, CTRL+Click Make OR from NAND Gates
In options, check European Resistors and uncheck Conventional Current.
Click the Inputs to see it working

Alternatively view OR_from_NAND.txt.
Save or copy the text on the web page. Import the saved or copied text into the Falstad simulator.

Here is the new HTML5 Simulator Site.

Boolean Algebra - AS Only

BOOLE: A mathematician called Boole invented a branch of maths for processing true and false values instead of numbers. This is called Boolean Algebra. Simple Boolean algebra is consistent with common sense but if you need to process decisions involving many values that might be true or false according to complex rules, you need this branch of mathematics. Boolean algebra was invented long before the invention of logic gates!

Logic Gate Rules

There are several types of gate. Each follows a very simple set of rules. By combining many gates in suitable ways, processing devices can be produced. A computer CPU chip can have millions of gates fabricated onto it. The table below shows several gates with two inputs. Many of these gates are also available in three, four and eight input versions.

Computers work using LOGIC. Displaying graphics such as the mouse cursor involves the XOR (Exclusive OR) operation. Addition makes use of AND and XOR.

Truth Tables

The one line descriptions of the rules below are clearer if shown in Truth Tables. These tables show the output for all possible input conditions. The inputs are always listed in the same order (counting in binary starting from zero).

Half Adder

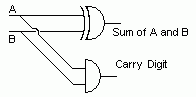
This is one of the simplest logic circuits that does something useful. It adds two bits together.

A      B   C S
0 plus 0 =   0
0 plus 1 =   1
1 plus 0 =   1
1 plus 1 = 1 0

The S or Sum column is identical to the XOR gate rule so this gate can be used.
The C or Carry column stores the result of adding 1 plus 1 giving 10 (two in binary), the AND gate can be used to generate this output.
By combining two half adders, a full adder can be made.
By combining 32 full adders, you are part way to building your first CPU chip for a fully featured computer.