Karnaugh Maps |
|
To gain access to revision questions, please sign up and log in.
A common type of control system uses a binary counter which counts from 0 to 15. When the counter reaches a particular number, the control system performs a suitable action. These control systems produce long, complicated Boolean expressions and complex circuits. Often the circuits can be simplified a lot.
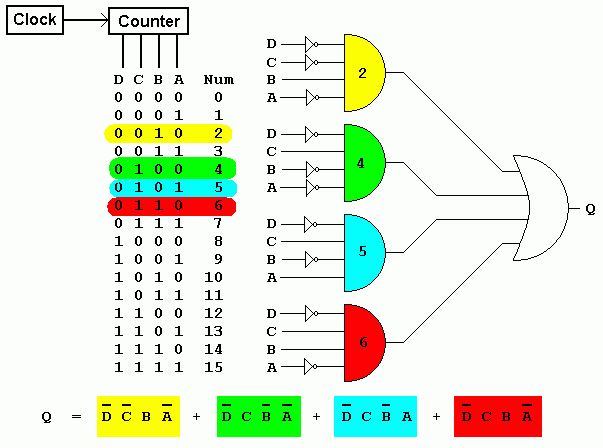
The circuit below is designed to operate a machine whenever the counter reaches 2, 4, 5 or 6.

In this circuit, the AND gates are wired up to DECODE or respond to particular numbers. They are colour coded and labelled to show which number. The rows in the table have matching colour codes. The Boolean expression is also colour coded to show which part of the expression matches each number or row in the table.
In plain English, the circuit detects 2, 4, 5 or 6.
In the Karnaugh map, ONEs are positioned in the squares that match the binary row numbers in the table. These have been colour coded to show which is which. Whenever ONEs group horizontally or vertically, for example in pairs or fours, it is possible to simplify the logic of the circuit.
| B A | B A | B A | B A | |
| D C | 0 0 | 0 1 | 1 1 | 1 0 |
| 0 0 | 1 | |||
| 0 1 | 1 | 1 | 1 | |
| 1 1 | ||||
| 1 0 |
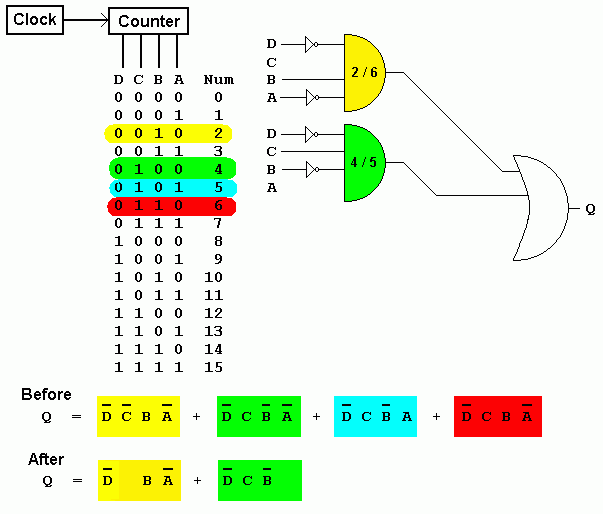
Looking at the Green (4) and Blue (5) squares, you can deduce that the value of A has no effect on that pair of squares. This means that the FOUR and FIVE detectors can be replaced with a single circuit and input A does not need to be wired up.
Similarly looking at the Yellow (2) and Red (6) squares, you can deduce that the value of C has no effect on that pair of squares. This means that the TWO and SIX detectors can be replaced with a single circuit and input C does not need to be wired up.
reviseOmatic V3 Contacts, ©, Cookies, Data Protection and Disclaimers Hosted at linode.com, London