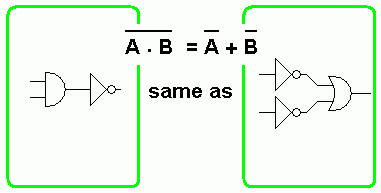
RANDOM PAGE
SITE SEARCH
LOG
IN
SIGN UP
HELP

Simplifying Logic

This is the AQA version closing after June 2019. Visit the the version for Eduqas instead .

To gain access to revision questions, please sign up and log in.

Techniques

If you have a good understanding of the logic gate rules, it is possible to work out a simpler solution just by examining the truth table and thinking hard. But this is a rather hit and miss approach and Karnaugh maps and Boolean algebra can be faster and more reliable methods but neither is easy.

Boolean algebra can be used to simplify expressions/circuits to generate a more optimal solution.

Logic Operations

+ means OR
. means AND
a line across the top means NOT
⊕ means XOR

De Morgan

A + B = A . B

A . B = A + B

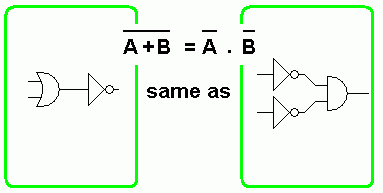
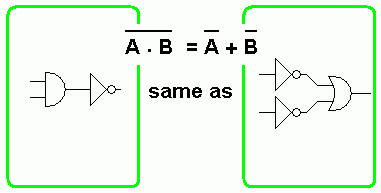
De Morgan

A + B = A . B
A . B = A + B

Gate Behaviour

AND GATE
- A . 1 = A The gate is open.
- A . 0 = 0 The gate is closed - output low.
OR GATE
- A + 1 = 1 The gate is closed - output high.
- A + 0 = A The gate is open.

Commutative

When using AND and OR, it makes no difference if the inputs are swapped.
- A . B = B . A
- A + B = B + A

Associative

The presence or absence of brackets makes no difference.
- A . (B . C) = (A . B) . C = A . B . C
- A + (B + C) = (A + B) + C = A + B + C

Distributive

A . (B + C) = A . B + A . C
(A + B) . (A + C) = A + (B . C)

Identity

A + A = A
A . A = A
A . B + A . B = A
(A + B) . ( A + B) = A

Redundancy

In all these expressions, one of the items has no effect and can be removed.

A . (A + B) = A
A + A . B = A
0 . A = 0
0 + A = A
1 . A = A
1 + A = 1
A . A = 0
A + A = 1
A . (A + B) = A . B
A + A . B = A + B